Nachdem das Interesse nach dem ersten Beitrag zu Harkness so groß war und ich vielfach nach passenden  Aufgaben gefragt wurde, möchte ich direkt einen Beitrag nachliefern. Und der befasst sich genau damit: den möglichen Aufgaben für den Einsatz der Harkness-Methode.

Du wirst vielleicht überrascht sein, aber du wirst sehen, dass du gar keine anderen Aufgabenformate benötigst als du wahrscheinlich ohnehin bearbeitest.

Ich zeige dir im heutigen Beitrag Beispiele aus Stunden, die ich mit Harkness durchgeführt habe und erkläre dir für jede Aufgabe auch noch, was die Knackpunkte waren. Das gibt dir sicher einen guten Überblick über potenzielle Hürden, die es gemeinsam zu überwinden gilt.

Welche Aufgaben können für Harkness verwendet werden?

Vielleicht ist der ein oder andere jetzt überrascht, aber es geht hier nicht darum, neue Aufgaben oder Aufgabentypen zu entwickeln und zu nutzen. Die typische Schulbuchaufgabe, die man sowieso im Unterricht behandeln würde, reicht für den Einsatz völlig aus. Das einzige, was sich verändert, ist das Setting drum herum.

Wichtig ist: Die Aufgabe muss mit dem Wissen der Schüler:innen lösbar sein. Das bedeutet nicht, dass sie keine Hilfsmittel benötigen dürfen und alles aus dem Kopf wissen müssen. Damit wäre es ja auch kein gemeinsames Problemlösen mehr.

Sie dürfen bei der Problemlösung auf alles zurückgreifen, was da ist: Bücher, Unterlagen, Smartphones, Tablets – je nachdem, was ihr an der Schule zur Verfügung habt.

Nach der Einführung eines neuen Themas folgt üblicherweise ja eine Übungsphase, in der eine Routine aufgebaut werden muss. Oder es findet ein Übergang zu Kontextaufgaben statt, der immer ein riesiger Schritt ist. Hier können wir mit der Harkness-Methode und Aufgaben perfekt ansetzen.

Beispiel 1: Aufgabenroutine

Als erstes gebe ich euch ein Beispiel, in dem es um das Erlangen von Routine geht. Das Thema war die Rekonstruktion von Funktionen. Ich habe dem Kurs dabei vier mögliche Aufgaben vorgelegt und ihnen erklärt, dass die Nummerierung mit fortschreitendem Schwierigkeitsgrad einhergeht. Ziel der Stunde war es, zwei der vier Aufgaben zu lösen. Die Aufgaben, die die Lerngruppe lösen wollte, konnten frei ausgewählt werden. In meiner Stunde wurden dabei eine leichtere und eine schwere Aufgabe gelöst.

Die vier Aufgaben waren dabei Standard-Aufgaben, ohne Kontext:

  1. Bestimmen Sie die Gleichung einer ganzrationalen Funktion f mit den angegebenen Eigenschaften: Grad 4, Sattelpunkt im Ursprung, Tiefpunkt T ( -2 | 6 ).
  2. Bestimmen Sie die Gleichung einer ganzrationalen Funktion f mit den angegebenen Eigenschaften: Grad 3, Tiefpunkt T ( 1 | -2 ), symmetrisch zum Koordinatenursprung.
  3. Bestimmen Sie die Gleichung einer ganzrationalen Funktion f mit den angegebenen Eigenschaften: Grad 4, Wendepunkt W ( -1 | -3 ), Extremum im Ursprung, die Wendetangente schneidet die y-Achse in Q ( 0 | 2 ).
  4. Bestimmen Sie die Gleichung einer ganzrationalen Funktion f mit den angegebenen Eigenschaften: Grad 3, f hat die gleichen Nullstellen wie die Funktion g(x)= x² – x – 2, Steigung im Punkt P ( 0 | -1 ) ist m = -3.

Hürden bei Beispiel 1

Wenn man die Aufgaben betrachtet, sieht man, dass das Erkennen der benötigten Bedingungen kleinere oder größere Hürden darstellt. Insbesondere in den Aufgaben 3 und 4 werden komplexere Bedingungen aufgegriffen: Der y-Achsenabschnitt der Wendetangente, Nullstellen anderer Funktionen oder die Steigung in einem Punkt.

Die Aufgaben 1 und 2 sind perfekt geeignet, um einen Einstieg in die Rekonstruktion zu bekommen und sich mit dem Vorgehen vertraut zu machen. Durch den steigenden Schwierigkeitsgrad kann die Gruppe, je nachdem, wie sie zurechtkommt, Aufgaben im entsprechenden Schwierigkeitsgrad auswählen.

Im Verlauf der Rekonstruktion kommen dann noch lineare Gleichungssysteme hinzu, deren Lösungen von jeher fehlerbehaftet und nicht zu unterschätzen sind.

Meine Lerngruppe wählte übrigens die Aufgaben 1 und 3. Erfolgreich!

Beispiel 2: Kontextaufgaben

Extremwertaufgaben kommen häufig mit Kontext einher. Prinzipiell werden diese Aufgaben meistens als schwierig empfunden und benötigen viel Übung.

Nach einem Einstieg in die Thematik, die als Hausaufgabe zu erledigen war, sind diese Aufgaben die ersten Übungen zum Thema gewesen. Dabei wird im Einstieg ein zweidimensionales Beispiel gewählt. Darauf folgend wird eine weitere Aufgabe aus zweien ausgewählt, die sich dann thematisch im dreidimensionalen Bereich befinden.

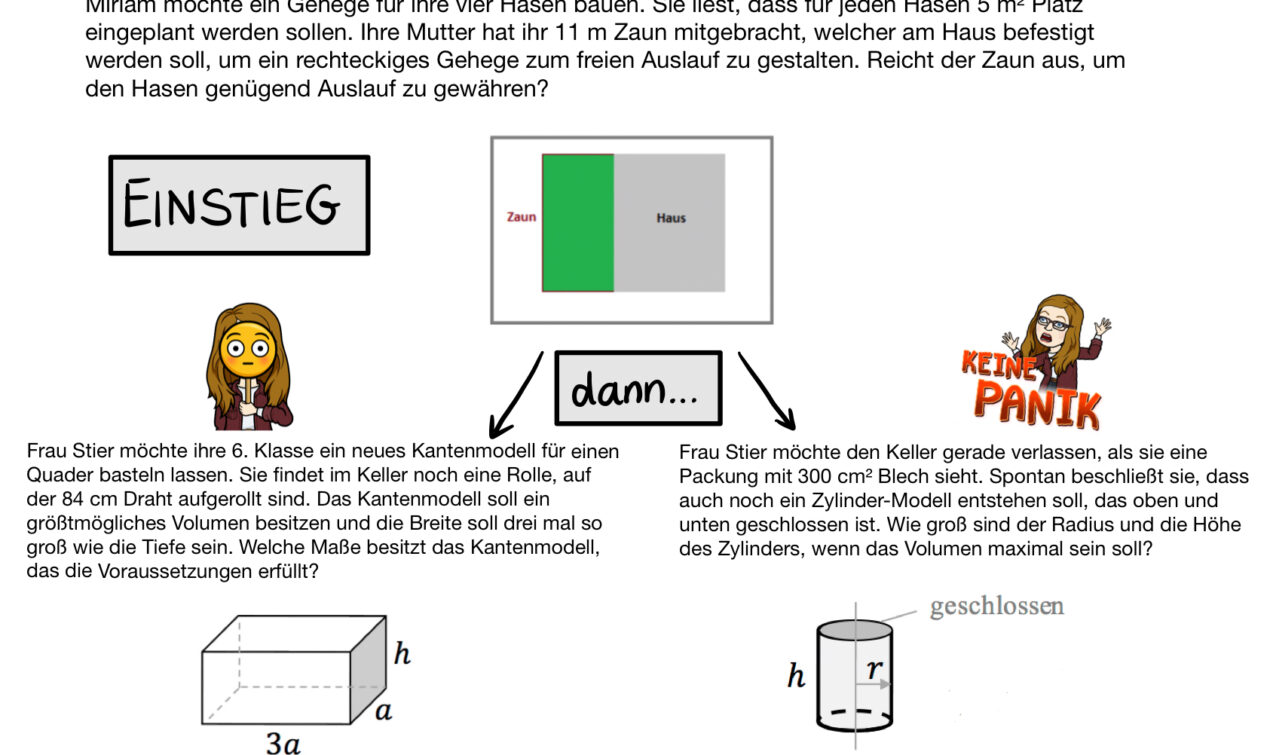
Harkness-Methode

Hürden bei Beispiel 2

Es handelt sich bei allen Aufgaben um Anwendungsaufgaben, die einem Kontext entstammen und ordentlich gelesen werden müssen. Gerade bei Extremwertaufgaben müssen dem Kontext grundlegende Informationen entnommen werden. Werden sie falsch herum interpretiert, verändert sich die gesamte Aufgabe.

Bei der Einstiegsaufgabe ist eine zusätzliche Stolperfalle, dass nicht der Umfang des gesamten Rechtecks verwendet werden muss, sondern nur drei Seiten benötigt werden.

Wählt man als zweite Aufgabe den Quader, müssen die Seitenlängen genutzt und das Volumen korrekt bestimmt werden. Dafür werden grundlegende Kenntnisse aus dem Rechnen mit Termen benötigt, die erfahrungsgemäß fehlerbehaftet sind.

Wählt man als zweite Aufgabe den Zylinder, kommen Pi und Volumen- und Oberflächenformeln ins Spiel. Darin fehlt häufig die Routine, was zu Unsicherheit in der Bearbeitung führen kann.

Beispiel 3: Kontextaufgaben

Das letzte Beispiel sieht so einfach aus, steckt aber voller Stolpersteine. Wir befinden uns im Bereich der Kurvendiskussion und dann im Bereich der Anwendungsaufgaben.

Die Interpretation der gegebenen Informationen ist die größte Hürde, aber nicht die einzige. Für die Lösung müssen wichtige Informationen korrekt gelesen werden. Dass „ohne Knick“ ein Codewort für die Wendetangente ist und x<-1 nicht bedeutet, dass man irgendeinen Wert kleiner als -1 wählen darf. Nicht zuletzt sind die Werte, die man beim Rechnen erhält, so krumm, dass die Schüler:innen zwischendurch keinen Anlass haben, sich der Richtigkeit der Ergebnisse sicher zu sein.

Du siehst: Da steckt eine Menge Diskussionsstoff drin. Und genau das konnte ich auch feststellen. Die Aufgabe war folgende:

Ein Straßenstück wird durch die Gleichung y = 0,1 x² – 0,6 x + 2,9 beschrieben. Die Straße soll für x<-1 geradlinig ohne Knick weitergeführt werden. Berechnen Sie die Gleichung der Geraden, die das weitergeführte Straßenstück beschreibt.

Hürden bei Beispiel 3

Ich würde behaupten, die Stunde, in der ich diese Aufgabe hineingab, war die spannendste meiner Harkness-Stunden.

Die Wendetangente war allen zwar ein Begriff, das Codewort „ohne Knick“ in dem Zusammenhang aber nicht. Wir hatten auch noch keine Gleichungen für Wendetangenten bestimmt. Dass dafür die einfache Geradengleichung herhalten kann, darauf muss man erstmal kommen.

Die größte Diskussion entfachte aber die Information x<-1. Die eine Seite war sich sicher, dass x=1 eingesetzt werden müsste. Die andere Seite war sich genauso sicher, dass das < darauf hinweist, dass x=1 gerade nicht herangezogen werden darf. Ich habe die, teilweise recht hitzige, Diskussion eine ganze Weile laufen lassen und beobachtet. Sie führte aber nicht zu einer Lösung, beide Seiten hielten an ihren Argumenten und Positionen fest und eine Lösung oder wenigstens ein Fortschreiten der Diskussion waren selbst nach 15 Minuten nicht in ansatzweise in Sicht.

An dieser Stelle habe ich das erste Mal in einer Harkness-Stunde eingreifen müssen. Ich habe gar nichts gesagt, aber als stummen Impuls eine Skizze an die Tafel gezeichnet. Daraufhin wurde diese von allen interpretiert und es ging korrekt weiter.

Fazit

Du siehst vielleicht, dass ich am Anfang nicht gelogen habe: Du kannst im Zusammenhang mit der Harkness-Methode deine ganz normalen Aufgaben verwenden und musst keine Extra-Aufgaben erstellen.

Worin die Hürden in Aufgaben liegen können, ist so individuell wie jede Lerngruppe und auch stark vom Fach abhängig. Du als Lehrkraft kannst sicher ziemlich genau entscheiden, worin Stolperfallen für deine Schüler:innen liegen und welche überwunden werden können und welche nicht.

Es muss auch keine umfangreiche, komplexe Aufgabe sein, um ausreichend Diskussionsbedarf hervorzurufen und die kollaborative Problemlösung zu fördern. Nicht selten reichen Mini-Hürden, um eine tolle Gruppendynamik beobachten zu können.

Also trau dich: Nimm dir doch einfach die nächste Aufgabe, die du ohnehin bearbeiten wolltest, und teste es mal aus!

Und weil es dazu einfach so viele Fragen gab und auch so viel zu erzählen gibt, werde ich noch zwei weitere Beiträge dazu veröffentlichen. Dabei wird es um den Umgang mit ruhigen Schüler:innen und nochmal genauere Hinweise zu möglichen Interaktionen der Lehrkraft gehen. Ich freue mich über eure Gedanken zum Thema.

Wenn dir mein Beitrag gefällt, freue ich mich, wenn du auf meinen Profilen auf Instagram, YouTube oder Facebook vorbeischaust. 

Diesen Beitrag teilen: